MaTeMaTiK DeHaSı - Matematik Teorem-İspat

MODELLEN KURAMI

Modeller kuramı, matematiksel konseptleri küme kuramı temelinde inceleyen ya da başka bir deyişle matematiksel sistemlerin dayandığı modelleri araştıran matematik dalıdır. Modeller kuramı, 'dış dünyada' matematiksel nesnelerin var olduğunu varsayar ve nesneler, nesneler arasında bazı işlemler ya da bağıntılar ve bir aksiyomlar kümesi verildiğinde, nelerin nasıl tanıtlanabileceğine ilişkin sorular sorar.

Seçim aksiyomu ve süreklilik hipotezinin küme kuramının diğer aksiyomlarından bağımsız olduğu tespiti modeller kuramından doğan en ünlü sonuçlardır (Paul Cohen ve Kurt Gödel tarafından tanıtlanmıştır). Hem seçim aksiyomunun hem de seçim aksiyomu negasyonunun küme kuramının Zermelo-Fraenkel aksiyomlarıyla uyumlu olduğu tanıtlanmıştır. Bu sonuçlar model teorisinin özel bir uygulaması olan Aksiyomatik küme kuramı dalının bölümleridir.

Modeller kuramının pratik bir uygulama örneği reel sayılar kuramıyla verilebilir. Her nesnenin bir reel sayı olduğu bir nesneler kümesi ve {×,+,-,.,0,1} gibi bir bağıntılar ve/ya da fonksiyonlar kümesini ele alalım. Bu dilde kuracağımız örneğin "∃ x (x × x = 1 + 1)" önermesinin reel sayılar için doğru olduğu yani belirtilen koşulu sağlan bir x olduğu bellidir; fakat aynı önerme rasyonel sayılar için yanlıştır. Buna karşın "∃ x (x × x = 0 - 1)" önermesi reel sayılar için yanlıştır. Önermeyi doğru yapmak için sabit bir simge i ve yeni bir aksiyom "i × i = 0 - 1" ekleyerek kompleks sayıları tanımlayabiliriz.

Buna göre modeller kuramı matematiksel sistemler içinde nelerin tanıtlanabilir olduğu ve bu sistemlerin kendi aralarındaki ilişkilerle ilgilenir. Özel olarak modeller kuramı bir sisteme yeni aksiyomlar ya da yeni dil yapıları eklendiğinde ne gibi sonuçlar ortaya çıktığını araştırır

KATEGORİ TEORİSİ

Bir kategori birbirileriyle ilişkili matematiksel nesneler sınıfının (örneğin grupların) özünü yakalamaya çalışır. Geleneksel olarak yapıldığı gibi tekil nesneler (gruplar) üzerine yoğunlaşmak yerine, bu nesneler arasındaki yapı muhafaza edici gönderimler (yani morfizimler) üzerine yoğunlaşır. Gruplar örneğinde bu gönderimler grup homomorfizmleridir. Bu şekilde farklı kategorileri funktorlar aracılığıyla ilişkilendirmek mümkündür.

Funktorlar, bir kategorinin her nesnesini diğer kategorinin bir nesnesiyle ve bir kategorideki morfizmi diğerindeki bir morfizme ilişkilendiren fonksiyonların bir genelleştirmesidir. Sıkça topolojik uzayın temel grubu gibi "doğal yapılar" funktorlar şeklinde ifade edilebilir. Bunun ötesinde, bu tip yapılar "doğal bir bağıntıya" sahiptir ve bir funktoru diğerine ilişkilendirme yolu olan doğal transformasyon konseptine olanak tanır.

Kategoriler, funktorlar ve doğal transformasyonlar Samuel Eilenberg ve Saunders MacLane tarafından 1945 yılında ortaya atılmıştır. Başlangıçta bu nosyonlar, topolojide, özellikle cebirsel topolojide, geometrik ve sezgisel bir kavram olan homolojiden aksiyomatik bir yaklaşım olan homoloji teorisine geçişte önemli bir bölümdür. Başkalarının yanı sıra Ulam tarafından (ya da kendisine atfen), benzer düşüncelerin 1930'ların sonunda Polonya okulunda ortaya çıktığı iddia edilmiştir.

Eilenberg/MacLane, kendi ifadelerine göre, bu kuramı geliştirirken doğal transformasyonları anlama çabasındaydılar. Bunu yapabilmek için funktorlar tanımlamak, funktorları tanımlamak için ise kategoriler tanımlamak gerekiyordu.

Günümüzde bu kuram, matematiğin tüm alanlarında uygulanmaktadır.

MATEMATİKSEL TANIT

Matematikte tanıt (belgit, ispat), ilgilenilen bir önermenin, belirli aksiyomlar esas alınarak, doğru olduğunu gösterme yöntemidir.Matematiksel tanıtta mantık kullanılır ancak genellikle bir ölçüde doğal dilden de yararlanılır ve dolayısıyla bir parça belirsizlik içerir. Gerçektende matematikte yazılan tanıtların büyük çoğunluğu informel mantığın uygulaması olarak kabul edilebilir. Tamamıyla formel tanıtların ele alındığı tanıtlama teorisi bağlamında, bu tip tamamıyle formel olmayan tanıtlamalara "sosyal tanıtlama" denir.

Bu ayrım, günümüz ve geçmiş matematiksel uygulamaların, matematikte yarı görgücülüğün ve matematik folklorünün yoğun olarak incelenmesine yol açmıştır. Matematik felsefesi ise dilin ve mantığın tanıtlardaki rölü ve "dil olarak matematik" ile ilgilidir.

Kişinin formalizme olan yaklaşımından bağımsız olarak, doğru olduğu tanıtlanan sonuca teorem denir. Bu teorem, tamamıyla formel olan bir tanıtta son satırda yer alır ve tanıtın tümü, bu teoremin aksiyomlardan nasıl türetildiğini gösterir. Bir teorem tanıtlandıktan sonra başka önermeleri tanıtlamada kullanılabilir. Matematiğin temelleri adı verilen önermeler tanıtlanamayan ya da tanıtlanması gerekmeyen önermelerdir. Bunlar bir zamanlar matematik felsefecilerinin başlıca uğraşı alanıydı. Günümüzde ilgi odağı daha çok matematiksel uygulamalara, yani kabul edilebilir matematiksel tekniklere kaymıştır.

Bazı kabul görmüş tanıtlama teknikleri:

Doğrudan tanıtlama: Sonucun, aksiyomlar, tanımlar ve daha önceki savların mantıksal olarak birleştirilmesiyle elde edildiği yöntem.
Tümevarımla tanıtlama: Temel bir durumun tanıtlandığı ve bir tümevarım kuralı kulanılarak çok sayıda (sıkça sonsuz olan) başka durumların tanıtlandığı yöntem.
Olmayana ergi tanıtı (Reductio ad absurdum olarak da bilinir): Bir özelliğin doğru olması durumunda mantıksal bir çelişkinin doğacağı dolayısıyla özelliğin yanlış olduğunun gösterildiği yöntem.
Oluşturarak tanıtlama: İstenen özelliğe sahip somut bir örnek oluşturularak istenen özellikte bir nesnenin var olduğunun gösterildiği yöntem.
Tüketerek tanıtlama: Tanıtlanacak önermenin sonlu sayıda duruma bölünerek her birinin ayrı ayrı tanıtlandığı yöntem.

Olasılıkçı tanıtlama, olasılık teorisi yardımıyla istenen özellikte bir örneğin var olduğunun gösterildiği bir tanıtlama olarak anlaşılmalıdır, yani bir teoremin doğru "olabileceği" şeklinde değil. Bu ikinci türdeki uslamlamalara 'usayatkınlık tanıtı' denebilir; Collatz sanısı örneğinde bunun gerçek bir tanıtlamadan ne kadar uzak olduğu aşikardır. Olasılıkçı tanıtlama -oluşturarak tanıtlama dışında- varlık teoremlerini tanıtlamanın birçok yönteminden biridir.

Örneğin "f(X)'i sağlayan en az bir X var" önermesini tanıtlamaya çalışıyorsanız, bir varlık ya da oluşturmacı olmayan tanıt f(X)'i sağlayan bir X olduğunu tanıtlar fakat bu X'in nasıl elde edileceğini göstermez. Buna karşın oluşturmacı bir kanıt X'in nasıl elde edildiğini de gösterir.

Doğru olduğu düşünülen fakat henüz tanıtlanmayan bir önerme sanı (konjektür) olarak bilinir.

Bazı durumlarda, belirli bir önermenin verili bir aksiyomlar kümesinden tanıtlanamayacağı tanıtlanabilir; bkz. örneğin süreklilik hipotezi. Aksiyom sistemlerinin çoğunda, ne tanıtlanabilen ne de tanıtlanamayan önermeler bulunur

BAYES TEOREMİ

Bayes teoremi olasılık kuramı içinde incelenen önemli bir konudur. Bu teorem bir rassal değişken için olasılık dağılımı içinde koşullu olasılık]lar ile marjinal olasılıklar arasındaki ilişkiyi gösterir. Bu şekli ile Bayes teoremi bütün istatistikçiler için kabul edilir bir ilişkiyi açıklar. Bu kavram için Bayes kuralı veya Bayes kanunu adları da kullanılır. Ancak bazı istatistikçiler için Bayes teoremi özel olarak değişik bir önem de taşır. Felsefi temelde olasılık değerlerinin nesnesel bir özellik değil, gözlemcinin meydana çıkardığı subjektif bir değer olarak kabul eden subjektivist olasılık düşünürlerine göre Bayes teoremi, yeni kanıtlar ışığında olasılık değeri hakkındaki subjektif inanışların güncelleştirilip değiştirilmesini sağlayan temel bir gereçtir; yani sonsal bir yaklaşımın temelidir.

Olasılık teorisi içinde incelenen bir 'olay olarak B olayına koşullu bir A olayı (yani B olayının bilindiği halde A olayı) için olasılık değeri, A olayına koşullu olarak B olayı (yani A olayı bilindiği haldeki B olayı) için olasılık değerinden farklıdır. Ancak bu iki birbirine ters koşulluluk arasında çok belirli bir ilişki vardır ve bu ilişkiye (ilk açıklayan istatistikçi İngiliz Thomas Bayes (1702–1761) adına atfen) Bayes Teoremi denilmektedir.

Formel bir teorem olarak Bayes teoremi, olasılık kavramını inceleyen her türlü değişik felsefi temel fikre bağlı olan her türlü istatisikçi tarafından kabul edilir. Ancak olasılığı objektif bir değer olarak gören ve relatif çokluluk olarak tayin eden çoklulukçu (en:frequentist) ekolüne bağlı olan istatistikçiler ile sübjektivist (veya Bayes tipi) ekoline bağlı olan istatistikçiler arasında bu teoremin pratikte nasıl kullanılabileceği hakkında büyük bir fikir ayrılığı bulunmaktadır. Çoklulukcu ekolüne dahil olanlar olasılık değerlerini rastgele olaylarda meydana çıkma çokluluğuna göre veya anakütlenin altsetlerinin tam anakütleye orantısı olarak saptanması gerekeğini kabul etmektedirler. Bunlara göre yeni kanıtlar karşısında olasılık değerinin değişme imkânı yoktur. Bu nedenle çoklulukcu ekolü için Bayes teoremi sadece koşulluluklar arasında ilişkiyi gösterir ve bunun pratikte kullanılma gücü küçüktür. Halbuki sübjektivist ekolüne göre olasılık gözlemcinin sübjektif belirsizlik ifadesidir. Bu nedenle olasılık değeri sübjektif olup yeni kanıtlar geldikçe değiştirilebileceğine inanmakta ve böylece Bayes teoremini istatistik bir incelemenin temel taşı saymaktadırlar.

Bayes teoreminin ifade edilişi

Bayes teoremi bir stokastik sürec sırasında ortaya çıkan bir rastgele olay A ile bir diğer rastgele olay B (eğer B için kaybolmamış olasılık varsa) için koşullu olasılıkları ve marjinal olasılıkları arasındaki ilişkidir, yani

$P(A|B) = frac{P(B | A), P(A)}{P(B)}.$

Bayes teoremi formülü içinde bulunan her bir terime özel isimler verilmektedir:

P(A) terimine A için önsel olasılık veya marjinal olasılık adı verilir. Bu önseldir, çünkü B olayı hakkında önceden herhangi bir bilgiyi içermemektedir.

P(A|B) terimi verilmiş B için Anın koşullu olasılığı adını alır.

P(B|A) terimi verilmiş A için Bnin koşullu olasılığı adını taşır.

P(B) terimi B olayı için 'önsel' olasılıktır veya Bnin marjinal olasılığıdır ve matematiksel rolü normalize eden bir sabittir.

Bu şekildeki Bayes teoremini, fazla matematiksel olmadan, sezgiye dayanarak şöyle açıklayabiliriz: Bayes teoremi eğer B gözlemlenmis ise, A gözlemi hakkındaki inançların ne şekilde güncelleştirilebileceğini ortaya çıkartır.

Bayes teoreminin olabilirlilik terimleri ile ifadesi

Bayes teoremi olabilirlilik terimleri ile de şöyle ifade edilebilir:

$P(A|B) propto L(A | b), P(A).$

Burada L(A|b) terimi verilmiş sabit b için Anin olabilirliğidir ve L(A|B)/P(B) orantısına bazan standardize edilmis olabilirlilik veya normalize edilmiş olabilirlilik adı da verilir. Böylece

$P(B | A) propto L(A | B)$

ilişkisini kullanarak Bayes teoremi ortaya çıkartılır. Bu sonucu sözcüklerle şöyle de yazabiliriz:

$mbox{sonsal} = {mbox{normalize olabilirlilik} times mbox{onsel}.}$

Daha uygun sözcüklerle

Sonsal olasılık önsel olasılık ile olabilirlilik çarpımına orantılıdır.

Koşullu olasılıklar kullanılarak matematiksel ispat

Bu teoremi ispat etmek icin koşullu olasılık tanımından başlanır. B olayı bilinirse A olayının olasılığı şöyle verilir:

$P(A|B)=frac{P(A cap B)}{P(B)}.$

Aynı şekilde A olayı verilmiş ise B olayının olasılığı şudur:

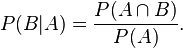
$P(B|A) = frac{P(A cap B)}{P(A)}. !$

Bu iki denklem yeniden düzenlenip birbirlerine birleştirilirse,

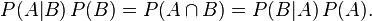
$P(A|B), P(B) = P(A cap B) = P(B|A), P(A). !$

ifadesi bulunur. Bu lemma bazan olasılıklar için çarpım kuralı olarak anılmaktadır. Her iki taraf da P(B) (eğer sıfır değilse) ile bolunurse, ortaya çıkan şu ifade Bayes teoremidir:

$P(A|B) = frac{P(B|A),P(A)}{P(B)}. !$

Bayes teoreminin değişik şekilleri

Bayes teoremi çok kere daha ek kavramlar eklenerek, sanki daha süslü olarak, ifade de edilir. Bunun için önce şu ifade kullanılır:

$P(B) = P(Acap B) + P(A^Ccap B) = P(B|A) P(A) + P(B|A^C) P(A^C),$

Burada A^C (çok kere A olmayan olarak ifade edilen) A olayının tamamlayıcısı olur. Bu Bayes teoremi formulüne konulunca Bayes teoremi için yeni alternatif bir formül elde edilir:

$P(A|B) = frac{P(B | A), P(A)}{P(B|A) P(A) + P(B|A^C) P(A^C)}. !$

Daha genel olarak, {A_i} olay uzayının bir bölüntüsünü oluşturduğu göz önüne alınca, bu bölüntü içinde bulunan herhangi bir A_i için şu ifade elde edilir:

$P(A_i|B) = frac{P(B | A_i), P(A_i)}{sum_j P(B|A_j),P(A_j)} , !$

Toplam olasılık yasası maddesine de bakınız.

Bahis oranı ve olabilirlilik orantısı şeklinde Bayes teoremi

Bayes teoremi çok daha düzgünce bir olabilirlik orantısı olan λ ile bahis oranı olan O terimleri ile şöyle ifade edilir:

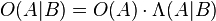
$O(A|B)=O(A) cdot Lambda (A|B)$

Burada

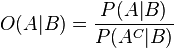
$O(A|B)=frac{P(A|B)}{P(A^C|B)} !$

B verilimişse A olayının bahis oranı;

$O(A)=frac{P(A)}{P(A^C)} !$

A kendi bahis oranı ve

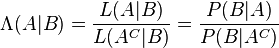
$Lambda (A|B) = frac{L(A|B)}{L(A^C|B)} = frac{P(B|A)}{P(B|A^C)} !$

olabilirlik orantısı olur.

Olasılık yoğunluk fonksiyonları ile Bayes teoremi

Bayes teoreminin sürekli olasılık dağılımlarına uygun olan bir şekli de vardır. Olasılık yoğunluk fonksiyonları tıpatıp olasılık olmadıkları için bu şeklin isbatı biraz daha karmaşıktır. Bu şekilde Bayes theoremi bir limit işlemin geliştirilmesi sonucu ile ortaya çıkarlar. ^[1].

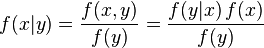
$f(x|y) = frac{f(x,y)}{f(y)} = frac{f(y|x),f(x)}{f(y)} !$

Buna benzer olan bir diğer ifade de toplam olasılık yasası için şöyle ortaya çıkartılabilir:

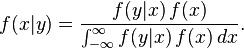
$f(x|y) = frac{f(y|x),f(x)}{int_{-infty}^{infty} f(y|x),f(x),dx}. !$

Aynı genel aralıklı hâl gibi bu formülde bulunan parçalara da özel isimler verilmiştir:

f(x, y) X ve Y için bileşik dağılımdır;

f(x|y) Y=y verilmiş iken X in sonsal dağılımıdır;

f(y|x) = L(x|y) (x in bir fonksiyonu olarak) Y=y verilmiş ise Xin olabilirlilik fonksiyonudur;

f(x) Xin marjinal dağılımı ve ve Xin önsel dağılımı olur;

f(y) Yin marjinal dağılımı olur.

Dikkat edilirse burada biraz alışılmış notasyon karışıklığı kavramına kendimizi kaptırdık. Burada her bir terim icin f notasyonu kullanıldı ama gerçekte bunlarin hepsi değişik birer fonksiyonlardir. Burada verilen hali ile fonksiyonların birbirinden değişik olduklar ancak içlerinde bulunan terimlerin farklı olmaları ile anlaşılabilmektedir.

Soyut Bayes teoremi [değiştir]

Olasılık uzayında verilmiş olan iki mutlak sürekli olasılık ölçümleri $P ˜ Q$ $(Omega, mathcal{F})$ ve bir sigma-cebiri $mathcal{G} subset mathcal{F}$ olsun. Bu halde $mathcal{F}$ -ölçülmeli rassal değişken $X$ için soyut Bayes teorem şöyle ifade edilir:

$E_P[X|mathcal{G}] = frac{E_Q[frac{dP}{dQ} X |mathcal{G}]}{E_Q[frac{dP}{dQ}|mathcal{G}]}$ .

Bu formulasyon şekli Kalman filtreleme tekniğinde Zekai denklemleri bulmak için kullanılır. Bu şekil ayrıca finansman matematiği içinde numeraire değişmesi tekniklerinde uygulanır.

Bayes teoreminin kapsamının genişletilmesi

Ikiden daha fazla degisken kapsayan problemler icin de Bayes teoremine benzer teoremler olusturulabilir. Ornegin

$P(A|B,C) = frac{P(A) , P(B|A) , P(C|A,B)}{P(B) , P(C|B)}$

Bu Bayes teoreminin ve kosullu olasilik tanimlamasinin uzerine birkac islem yaparak ortaya cikarilabilir:

$P(A|B,C) = frac{P(A,B,C)}{P(B,C)} = frac{P(A,B,C)}{P(B) , P(C|B)} =$

$= frac{P(C|A,B) , P(A,B)}{P(B) , P(C|B)} = frac{P(A) , P(B|A) , P(C|A,B)}{P(B) , P(C|B)} .$

Bu calismalar icin uygulanacak genel strateji ortak olasilik icin parcalama ile calismaya baslayip ilgimizi cekmek istemedigimiz degiskenleri entregrasyon ile marginalize etmektir. Uygulanan parcalam sekline gore, bazi entegrallerin 1e esit olup parcalama ifadesinden dusmeleri sagmanma imkâni bulunabilir; eger bu ozellik ve imkân kullanilabilirse gereken hesaplamalar cok onemli sekilde azaltilabilir. Ornegin, bir Bayes tipi sebeke icin verilen spesifikasyon dolayisiyla, (geri kalan degiskenler verilmis olurlarsa) herhangi bir degisken icin kosullu olasilik, birkac degiskenli ortak dagilimin faktorize edilmesi ile belirlenir ve bu nedenle sonucun ozellikle basit bir form almasi saglanmis olur. (Markov battaniyesi maddesine bakiniz.)

Örneğinler

Örneğin #1: Koşullu olasılıklar

İki tabak dolusu biskui düşünülsün; tabak #1 içinde 10 tane çikolatalı biskui ve 30 tane sade biskui bulunduğu kabul edilsin. Tabak #2 içinde ise her iki tip biskuiden 20şer tane olduğu bilinsin. Evin küçük çocuğu bir tabaği rastgele seçip bu tabaktan rastgele bir biskui seçip alsın. Çocuğun bir tabağı diğerine ve bir tip biskuiyi diğerine tercih etmekte olduğuna dair elimizde hiçbir gösterge bulunmamaktadır. Çocuğun seçtiği biskuinin sade olduğu görülsün. Çocuğun bu sade biskuiyi tabak #1 den seçmiş olmasının olasığının ne olacağı problemi burada incelenmektedir.

Sezgi ile, tabak #1de sade biskui sayısının çikolatali buskui sayısına gore daha fazla olduğu göz önüne alınırsarak incelenen olasılığın %50den daha fazla olacağı hemen algılanır. Bu soruya cevap Bayes teoremi kullanarak kesin olarak verilebilir. Önce soruyu değiştirip Bayes teoremi uygulanabilecek şekle sokmak gerekmektedir: Çocuğun bir sade biskui seçmiş olduğu bilinmektedir; o halde bu koşulla birlikte tabak #1den seçim yapması olasığı ne olacaktır?

Böylece Bayes teoremi formülüne uymak için A olayı çocugun tabak #1den seçim yapması; B olayı ise çocugun bir sade biskui seçmesi olsun. İstenilen olasılık böylece Pr(A|B) olacaktır ve bunu hesaplamak için şu olasılıkların bulunması gerekir:

Pr(A) veya hiçbir diğer bilgi olmadan çocuğun tabak #1 den seçim yapması olasığı;

İki tabak arasında tercih olmayıp seçimin eşit olasığı olduğu kabul edilmektedir.

Pr(B) veya hiçbir diğer bilgi olmadan çocuğun bir sade biskui seçmesi olasığı: Diğer bir ifade ile, bu çocuğun her bir tabaktan bir sade biskui seçme olasığıdır. Bu olasılık, önce her iki tabaktan ayrı ayrı olarak secilen bir tabaktan bir sade biskui seçme olasıği ile bu tabağı seçme olasığının birbirine çarpılması ve sonra bu iki çarpımın toplanması suretiyle elde edilir. Tabaklarda olan sade biskuinin sayısının toplama orantısından bilinmektedir ki tabak #1den bir sade biskui seçme olasılığı (30/40=) 0,75; tabak #2den sade biskui seçme olasılığı (20/40=) 0,5 olur. Her iki tabaktan seçme olasılığı ise her tabak ayn sekilde uygulama gördüğü için 0,50 olur. Böylece bu problemin tümü için bir sade biskui seçme olasılığı 0.75×0.5 + 0.5×0.5 = 0.625 olarak bulunur.

Pr(B|A), veya çocuğun tabak #1den seçim yaptığı bilirken bir sade biskui seçmesi.: Bu 0,75 olarak bilinmektedir çünkü tabak #1deki toplam 40 biskuiden 30u sade biskuidir.

Şimdi bu aciklanan tüm olasılık değerleri Bayes teoremi formüne konulabilir:

$P(A|B) = frac{P(B | A) P(A)}{P(B)} = frac{0.75 times 0.5}{0.625} = 0.6$

Böylece çocuğun tabak #1den seçim yaptığı bilindiğine göre bir sade biskui seçimi yapmasının olasılığı %60dir ve sezgimize göre seçtiğimiz %50den daha büyüktür.

Ortaya çıkma tabloları ve orantısal çokluklar

Kosşullu olasılıkları hesaplarken her bir bağımsız değişken için her mümkün sonucun ortaya cikma sayısını veya her sonucun relatif çoklulukunu gösteren basit bir tablo hazırlamak konuyu daha iyi anlamaya yardımcı olabilir. Biskuvi örneği için bu yöntemin kullanışını gösteren tablolar şöyle verilmiştir:

Her tabakta bulunan değişik tip biskui sayısı Her tabakta bulunan değişik tip biskui oranları

Tabak #1 Tabak #2 Toplamlar

Çikolatalı 10 20 30

Sade 30 20 50

Toplam 40 40 80

Tabak #1 Tabak #2 Toplamlar

Çikolatalı 0.125 0.250 0.375

Sade 0.375 0.250 0.625

Toplam 0.500 0.500 1.000

Sağdaki tablo, sol taraftaki tablo içindeki her bir hücre elemanını toplam biskui sayısı (yani 80) ile bölerek elde edilmiştir.

Örneğin #2: Yeni ilaç sınamaları

Örneğin #3: Bayes tipi sonuç çıkartıcı analiz

Örneğin #4: Monty Hall problemi

Bir TV oyun programında üç tane (kirmizi, yesil ve mavi boyali) kapali kapi gosterilmekte ve bu kapilardan birinin arkasinda bir armagan bulunmaktadir. Kirmizi kapiyi sectigimizi dusunelim; ama bu kapi program sunucunun bir faaliyet goistermesini bitirmeden acilmamaktadir. Program sunucusu hangi kapi arkasinda armagan bulundugunu bilmektedir; ama ona verilen direktife gore ne arkasinda armagan bulunan kapiyi ne de sectigimiz kapiyi acabilir. Yesil kapiyi acar ve arkasinda bir armagan bulunmadigini gosterir ve su soruyu yarismaciya sorar: "Ilk tercihiniz olan kirmizi kapi hakkinda fikrinizi değistirmek ister misiniz?" Incelenecek sorun armaganin mavi veya kirmizi kapilar arkasinda bulunma olasiliklari nedir?

Yarismanin ana sonuclari olan degisik renkli kapilar arkasinda armagan bulunmasini soyle ifade edelim A_k, A_y ve A_m. Ilk olarak her bir kapi arkasinda armagan bulunmasi birbirine esit olasigi oldugu kaabul edilir yani $P(A_k) = P(A_y) = P(A_m) = frac 1 3$ oilur. Yine dusunelim kirmizi kapiyi yarismaci secmis durumdadir. "Sunucunun yesil kapiyi acmasi olayina B olayi adini verelim. Arkasinda armagan bulunan kapiyi bilmeseydi bu olay icin olasilik %50 olacaktir.

Eger gercekte armagan kirmizi kapi arkasinda ise, sunucu ya yesil ya da mavi kapiyi acmakta serbest olacaktir. Bu halde $P (B | A k) = 1 / 2$

Eger gercekte armagan yesil kapi arkasinda ise, sunucu mavi kapiyi acacaktir. Yani $P (B | A y) = 0$ .

Eger gercekte armagan mavi kapi arkasinda ise, sunucu yesil kapiyi acacaktir. Yani $P (B | A m) = 1$ .

Boylece

$begin{matrix} P(A_k|B) & = frac{P(B | A_k) P(A_k)}{P(B)} & = frac{frac 1 2 frac 1 3}{frac 1 2} & = frac 1 3 P(A_y|B) & = frac{P(B | A_y) P(A_y)}{P(B)} & = frac{0 frac 1 3}{frac 1 2} & = 0 P(A_m|B) & = frac{P(B | A_m) P(A_m)}{P(B)} & = frac{1 frac 1 3}{frac 1 2} & = frac 2 3 end{matrix}$

Dikkatle incelenirse bunun P(B) degerine bagli oldugu gorulecektir. Bir an armaganin kirmizi kapi arkasinda olmadığını farzedelim; o halde sunucunun yesil kapiyi acma olasigi cok yuksek olacaktir - diyelim %90. Bundan dolayi, eger sunucu baska kapi acmaya zorlanmadikca, yesil kapiyi acmayi tercih edecektir. Boylece, B olayi olasigi 1/3 * 1 + 1/3 * 0 + 1/3 * 9/10 = 19/30 olur.

$begin{matrix} P(A_k|B) & = frac{P(B | A_k) P(A_k)}{P(B)} & = frac{frac 9 {10} frac 1 3}{frac {19} {30}} & = frac 9 {19} P(A_y|B) & = frac{P(B | A_y) P(A_y)}{P(B)} & = frac{0 frac 1 3}{frac {19} {30}} & = 0 P(A_m|B) & = frac{P(B | A_m) P(A_m)}{P(B)} & = frac{1 frac 1 3}{frac {19} {30}} & = frac {10} {19} end{matrix}$

Bu nedenle sunucunun yesil kapiyi acmasi bizi cok az bilgi vermektedir - zaten bu secime yapamaga zorundadir. Pr(A_m) olasigi 1/2in cok az ustundedir.

Buna karsilik, armaganin kirmizi kapi arkasinda oldugunu farzedersek; o halde sunucunun yesil kapi acma olasigi cok kucuk olacaktir - diyelim %10. Bu demektir ki ozellikle zorlanmadikca sunucu nerede ise hic bir halde yesil kapiyi acmiyacaktir.

O halde B olasigi 1/3 * 1 + 1/3 * 0 + 1/3 * 1/10 = 11/30 olur

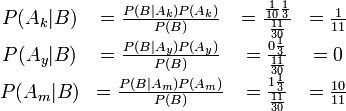
$begin{matrix} P(A_k|B) & = frac{P(B | A_k) P(A_k)}{P(B)} & = frac{frac 1 {10} frac 1 3}{frac {11} {30}} & = frac 1 {11} P(A_y|B) & = frac{P(B | A_y) P(A_y)}{P(B)} & = frac{0 frac 1 3}{frac {11} {30}} & = 0 P(A_m|B) & = frac{P(B | A_m) P(A_m)}{P(B)} & = frac{1 frac 1 3}{frac {11} {30}} & = frac {10} {11} end{matrix}$

Bu halde, gercekte sunucunun yesil kapiyi acmasi bize cok onemli bilgi vermektedir. Aramagan nerede ise hic suphesiz mavi kapi arkasinda bulunmaktadir. Eger mavi kapi arkasinda degilse sunucu cok muhtemelen mavi kapiyi acacakti

Bayes teoreminin ifade edilişi

Bayes teoreminin olabilirlilik terimleri ile ifadesi

Koşullu olasılıklar kullanılarak matematiksel ispat

Bayes teoreminin değişik şekilleri

Bahis oranı ve olabilirlilik orantısı şeklinde Bayes teoremi

Olasılık yoğunluk fonksiyonları ile Bayes teoremi

Soyut Bayes teoremi [değiştir]

Bayes teoreminin kapsamının genişletilmesi

Örneğinler

Örneğin #1: Koşullu olasılıklar

Ortaya çıkma tabloları ve orantısal çokluklar

Örneğin #2: Yeni ilaç sınamaları

Örneğin #3: Bayes tipi sonuç çıkartıcı analiz

Örneğin #4: Monty Hall problemi